Draw All Trees Up to Isomorphism
Graph Theory Simplified
Graph Theory | Isomorphic Trees
Hello all. We are here at the 10th post of my blog series on Graph Theory named Graph Theory : Go Hero. Today, we are diving into the isomorphism in trees. I strongly suggest you to read my recent posts on Graph Theory, which is more formatted in a Computer Science aspect. So, let's dig in.
Defining Isomorphism
Isomorphism is a very general concept that appears in several areas of mathematics. The word derives from the Greek iso, meaning " equal ," and morphosis, meaning " to form " or " to shape ." It represents the mutual relationship between two similar system. Wikipedia has got some great explanation on what is it and how it's useful in Mathematics. In a nutshell, it's a map between two objects. For instance, let's take an example of an isomorphism. Suppose that we have two sets of numbers. Two finite sets are isomorphic if they have the same number of elements. Said another way in a little more detail, two (now-not-necessarily-finite) sets are isomorphic if you can write down a function that assigns each element of one set to a unique element of the other set, such that no elements of either set are "missed" by the function.
Graph Isomorphism
The question of asking whether two graphs G1 and G2 are isomorphic is asking whether they are structurally same.
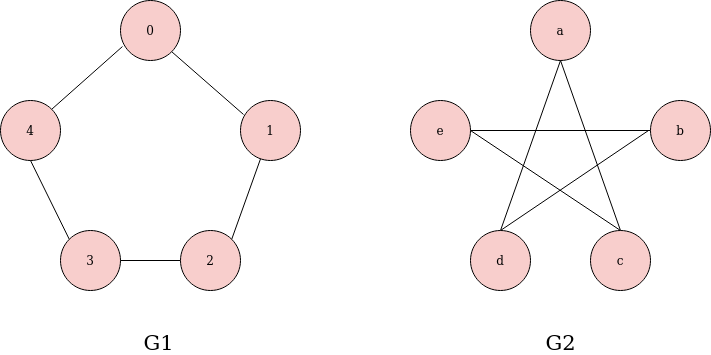
We can see two graphs above. Even though graphs G1 and G2 are labelled differently and can be seen as kind of different. But, structurally they are same graphs. So, in turn, there exists an isomorphism and we call the graphs, isomorphic graphs. If we unwrap the second graph relabel the same, we would end up having two similar graphs.
We can also define the notion of graph isomorphism in a more rigorous way because saying - two graphs are structurally the same - is not well defined. If we imagine a graph as a set of vertices V and edges E, we would have two sets G1 (V1, E1) and G2(V2, E2) for graphs G1 and G2 respectively. We call these two graphs isomorphic, if there exists a bijection between V1 and V2 such that for all the pairs vertices in G1 that form a valid edge by applying a function φ (phi) to the nodes of all edges result in edge which is present in G2. In layman's term,
for an isomorphism to take place, there needs to be a function φ which can map all the nodes/edges in G1 to G2 and vice-versa.
Determining if two graphs are isomorphic is not only obvious to human eyes, but also a difficult problem for computers.
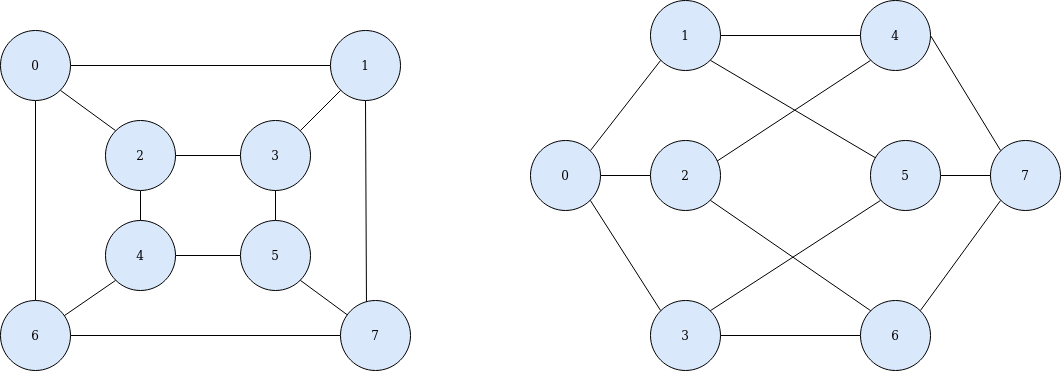
It is still an open question as to whether the graph isomorphism problem is NP complete . However, many polynomial time isomorphism algorithms exist fir graph sub classes such as trees.
Can you do it If I ask you to spot isomorphic trees? Yes, right? let's give it a try.
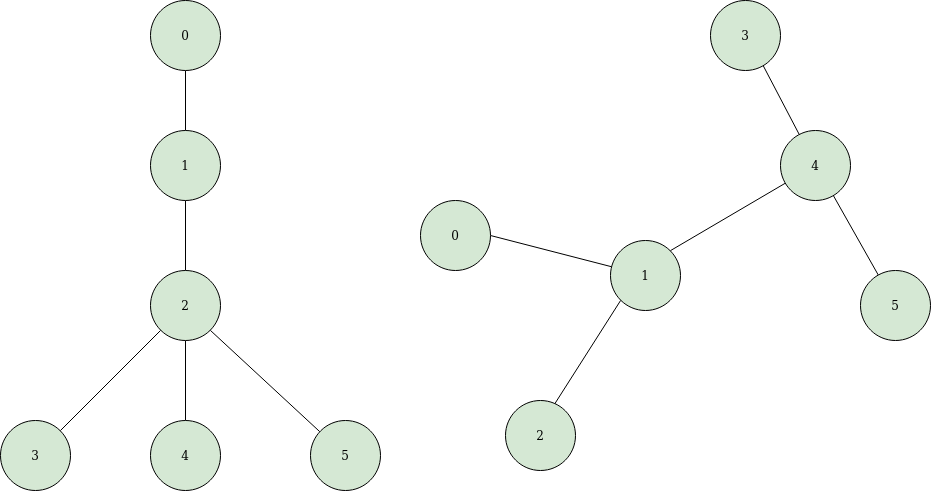
You are right, if you answered no. Because, they are not structurally same.
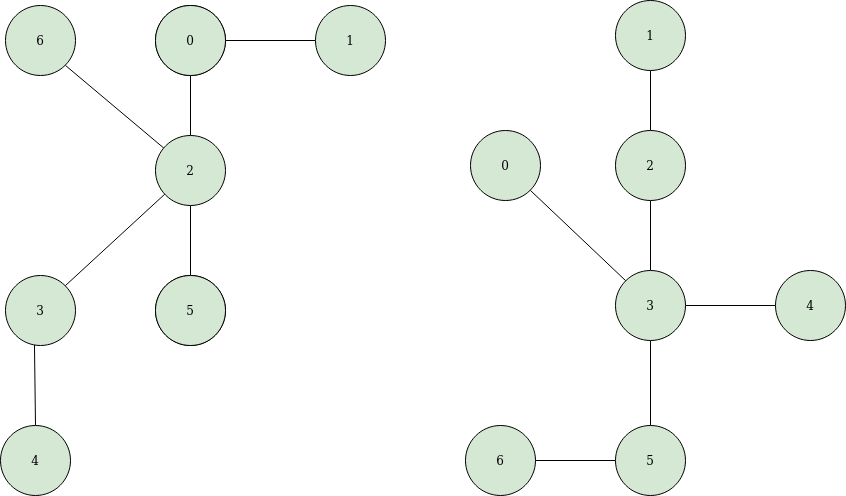
How about this?
The answer is yes. Because there exists a label map like
6 - 0
1 - 1
0 - 2
2 - 3
5 - 4
3 - 5
4 - 6
There are several very quick probabilistic (usually hash or heuristic based) algorithms for identifying isomorphic trees. These tend to be fast, but also error prone due to hash collisions in a limited integer space.
The method we will be looking at today involves serializing a tree into a unicode encoding . This unique encoding is simply a unique string that represents a tree, if another tree has the same encoding, then they are isomorphic.
We can directly serialize an unrooted tree, but in practice serializing a rooted tree is typically easier code wise. However, one caveat to watch out for if we are going to root our two trees T1 and T2 to check if they are isomorphic is to ensure that the same root node is selected in both trees before serializing/encoding the trees.
One trick we can use to help ourselves is to find a common node between both the trees. Finding the center of a tree would do the same.
Encoding a tree
First, let's take two trees T1 and T2 which may be isomorphic or not.
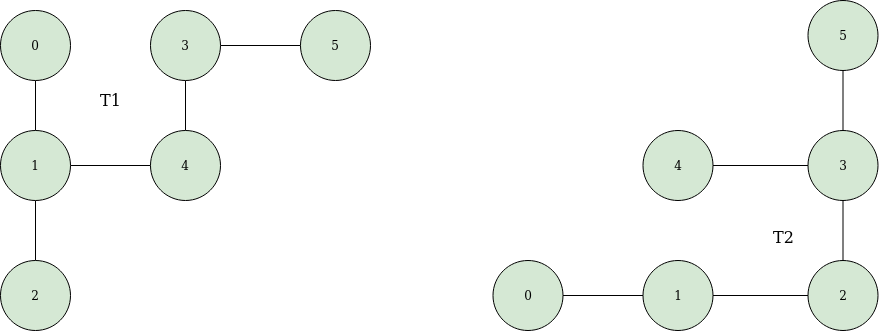
We have to find the centers of the trees.
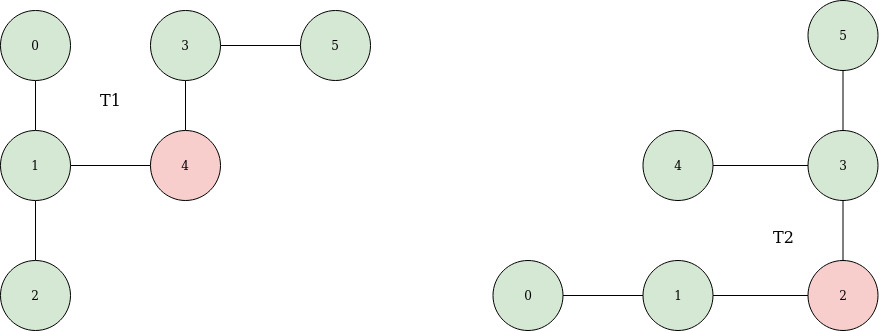
The next thing we have to do is rooting a tree.
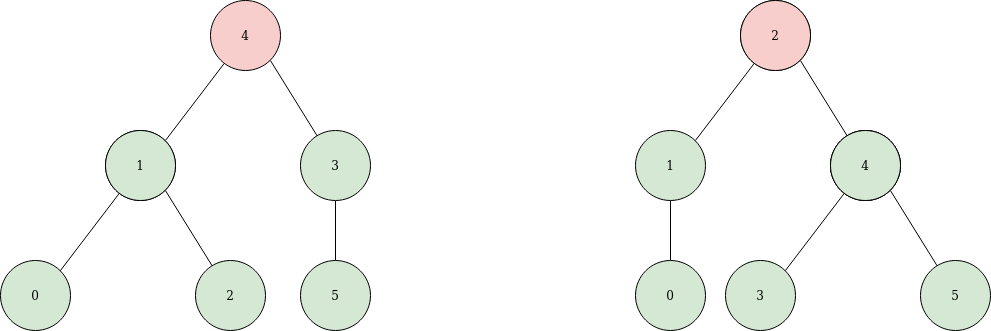
Now we have to generate the encoding for each tree and compare the serialized trees for equality.

The tree encoding is simply a sequence of left '(' and right ')' brackets. However, we can also think of them as 1's and 0's. The same above encoding could be converted to the suggested method as,

Generating the tree encoding
The AHU ( Aho , Hopcroft , Ullman ) algorithm is a clever serialization technique for representing a tree as a unique string. Unlike many tree isomorphism invariants and heuristics, AHU is able to capture a complete history of a tree's degree spectrum and structure ensuring a deterministic method of checking for tree isomorphism.
Let's have a closer look.
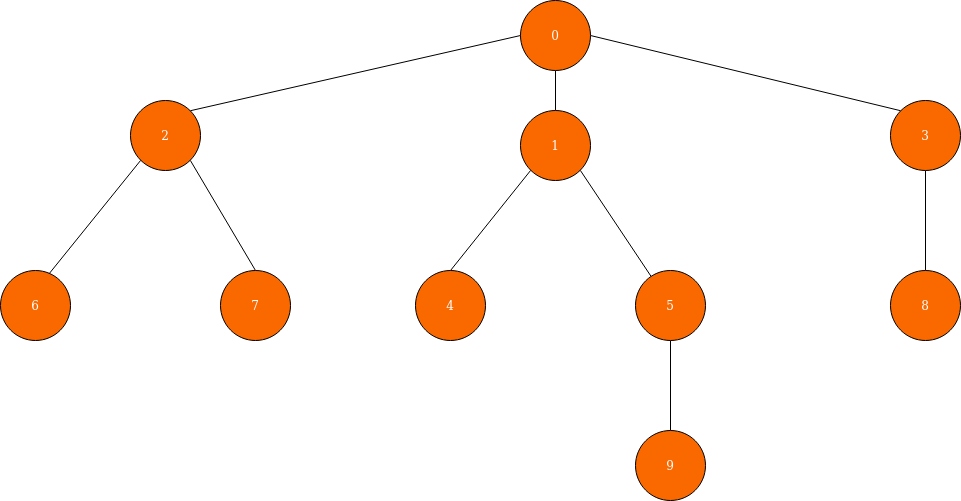
We have to get started by assigning an empty parenthesis ( () ) to every leaf node of our tree like below.
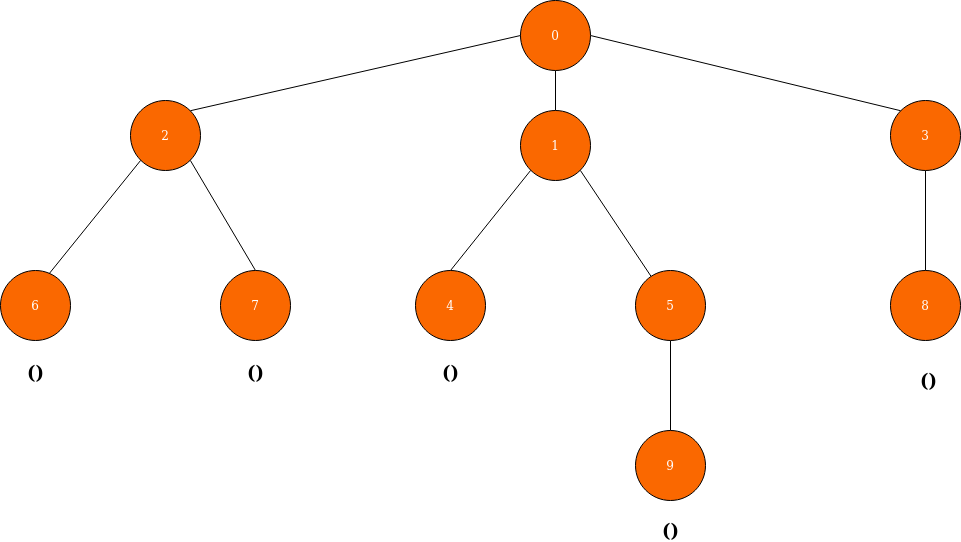
Now we have to move upwards (to the parent nodes of the leaves) and combine the parenthesis of the leaves together and assign it to the parent. As we combines leaves' parentheses, we should also wrap the result in another pair of parentheses. For example, suppose we have a tree with a single parent and two leaves. So we assign () to the leaves. When we move towards the parent node, we combine the parentheses of leaves like ()() and wrap it in another pair of parentheses like (()()) and assign it to the parent. This process continues iteratively until we reach the root node.
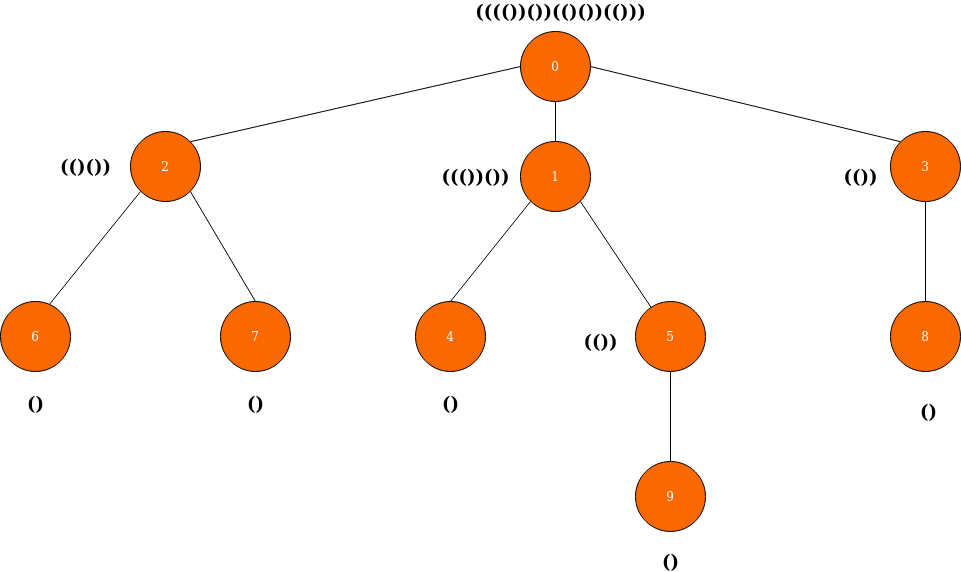
If you carefully follow the above analogy, we would have this encoding for the tree at the end.
Don't forget to sort the parentheses before combining it. Sorting is done lexicographically.
Encoding summary
In summary of what we did for AUH:
- Leaf nodes are assigned with ()
- Every time we move upwards, combine, sort and wrap the parentheses.
- We can't process a node until we have processed all its children.
Two trees are isomorphic if their representation is same.
Gotcha! I hope this brief would help you in your future projects. I appreciate your time and patience. Thank you.

kowalskireatect1992.blogspot.com
Source: https://towardsdatascience.com/graph-theory-isomorphic-trees-7d48aa577e46
0 Response to "Draw All Trees Up to Isomorphism"
Post a Comment